A Merkle tree represents a fundamental data structure in cryptography and distributed systems, implementing a hash-based binary tree that enables efficient and secure verification of large data sets.

Technical Architecture
A Merkle tree consists of a binary tree where each leaf node contains the cryptographic hash of a data block, while each non-leaf node contains the hash of its child nodes’ combined hashes. This structure creates a hierarchical arrangement of cryptographic proofs.
Computational Mechanism
The computational efficiency of Merkle trees stems from their logarithmic properties. For n data blocks, the tree height is log₂(n), making verification operations highly efficient. The space complexity remains O(n), as the tree requires storage proportional to the input data.
The process begins with the creation of leaf nodes by hashing individual data blocks. These hashes form the bottom layer of the tree. Moving upward, adjacent pairs of hashes are combined and hashed again to form parent nodes. This process continues until reaching a single root hash, which represents the entire data set.
Key computational characteristics include tree construction with linear time complexity, proof generation and verification with logarithmic time complexity, and linear storage overhead proportional to the input data size.
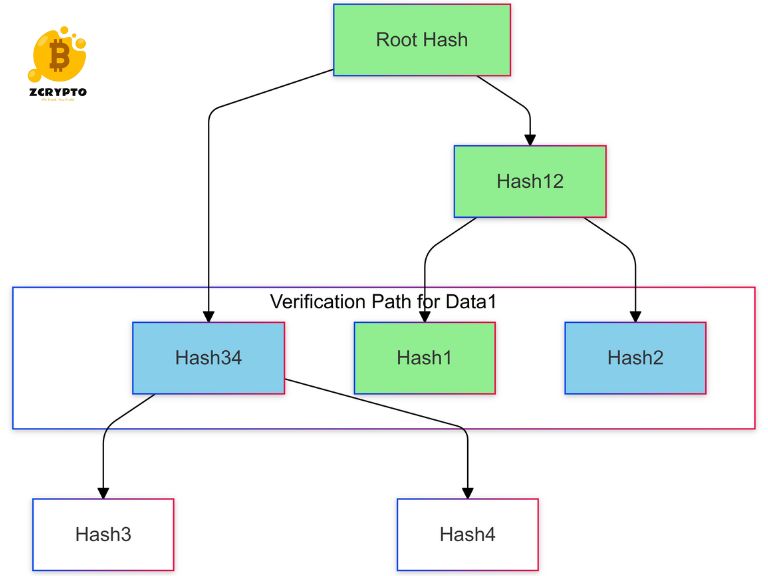
Verification Process
The verification process in Merkle trees follows a systematic approach that ensures data integrity. Starting with a specific data block, its hash is computed and combined with provided sibling hashes at each level of the tree. This process continues upward, reconstructing the path to the root. The final computed hash is compared with the known root hash to verify the data’s authenticity.
Each verification step involves:
- Computing the hash of the target data block
- Combining it with the corresponding sibling hash
- Hashing the combined value
- Repeating the process with the next sibling in the path
- Comparing the final result with the stored root hash
Security Properties
Merkle trees provide comprehensive security through several key mechanisms. The hash chaining structure ensures that any modification to data blocks results in a different root hash, making tampering evident. The system allows verification of specific data blocks without requiring access to the complete dataset.
The security features extend to:
- Immediate detection of data alterations through hash mismatches
- Efficient partial data verification capabilities
- Cryptographic linking between all data blocks
- Resistance to second preimage attacks
Technical Applications
Distributed Systems
In distributed environments, Merkle trees facilitate efficient data synchronization. Nodes can compare sections of their trees rather than entire datasets, significantly reducing network traffic and processing overhead. The hierarchical structure allows quick identification of discrepancies between datasets.
Blockchain Technology
Blockchain systems extensively utilize Merkle trees for transaction organization. The structure enables block header compression by storing only the root hash instead of all transaction hashes. This facilitates Simple Payment Verification (SPV), allowing lightweight clients to verify transactions without downloading the entire blockchain.
Version Control Systems
Version control systems employ modified Merkle tree structures to manage content changes. This enables efficient storage and verification of file histories while maintaining data integrity across distributed repositories.
Performance Considerations
Several factors affect Merkle tree performance:
The tree’s balanced structure ensures consistent performance across operations. Parallel processing capabilities allow simultaneous hash computations of independent branches. The system supports incremental updates, enabling efficient modification of existing trees without complete reconstruction.
Strategic caching of intermediate nodes can significantly improve verification speed. Branch pruning techniques reduce storage requirements while maintaining verification capabilities for active data.
Academic References
- Merkle, R. C. (1987). “A Digital Signature Based on a Conventional Encryption Function”
- Bayer, D., Haber, S., & Stornetta, W. S. (1993). “Improving the Efficiency and Reliability of Digital Time-Stamping”
- Crosby, S. A., & Wallach, D. S. (2009). “Efficient Data Structures for Tamper-Evident Logging”
Serves as a cornerstone of modern cryptographic systems, providing efficient verification mechanisms for large-scale distributed data structures while maintaining strong security properties through its hierarchical hash-based architecture.


